Science of best practices

There is a simple idea once told by Feynman — the purpose of physics is to seek the simplest theory that would describe as much of the natural phenomena as possible. That's the idea behind electrodynamics of Maxwell or QED. Each new grand theory was able to describe more of the world and at the same time be simple.

That is a beautiful idea with a very clear purpose which gives great results. So why we (software engineers) don't take it on and embrace it? Why some of the best ideas around engineering aren't yet formalized and unified, like the best practices such as KISS or DRY? Are they inherently not formalizable? It can't be true if we assume computer science is a branch of math. There should be some way to derive best practices. And maybe once we learn how to derive them we might learn how to derive new best practices that aren't yet established from empirical knowledge. We've seen this happen in other engineering fields, like with planes and airfoil. We've built planes from empirical knowledge and only after that the actual laws of aerodynamics were discovered which led to better planes with jet propulsion and so on.

This article is a handwavy attempt to indicate that there seems to be something underneath the best practices as we know them. I conjecture, all well-established best practices can be derived.

Categories

The mathematical basis of software engineering lays in the category theory and I don't mean the complex parts of it, but the most basic and simple subject. I'll to approach the general topic of formalization from that. To start, let's explore categories just a bit.

Category theory is a theory about categories, and categories are nothing more than a bunch of objects connected with arrows.

In software engineering, we're interested in a specific kind of category that is called a category of types. In a category of types, objects are actual types and arrows are functions between them.

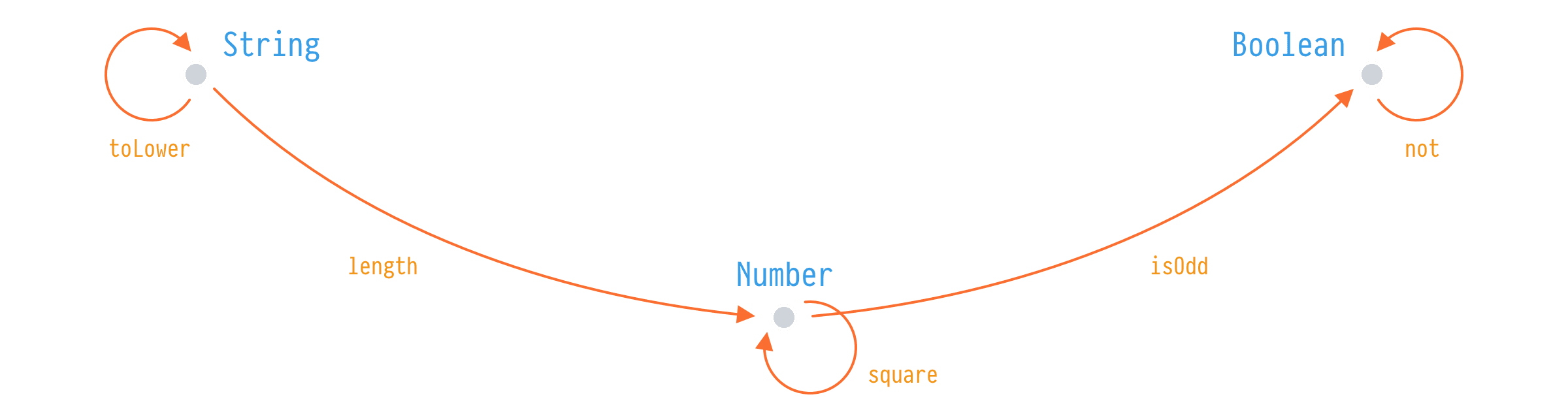
In this simple definition, we can make an observation that objects aren't relevant, they are just there to mark the start and end for the arrows. And if translated, types don't matter in a category, arrows do. Types are here for functions to have input and output. It's also not important how many arrows we have between objects. If we have 1, 2, or Infinity everything stays the same.

If we combine this observation with another great idea, we will have enough for rudimentary analysis. That other great idea is the composition.

Composition

In category theory, composition is the ability to derive a direct arrow between two objects when those objects are connected with indirect arrows.

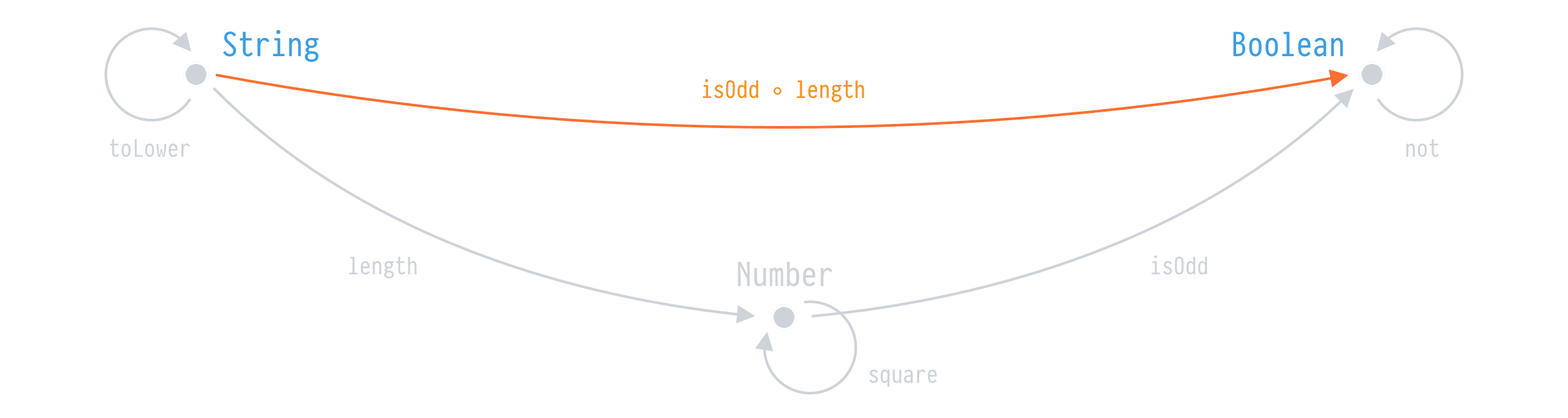
if we have the arrows length and isOdd between String, Number, and Boolean, we can compose these arrows to get a direct arrow isOdd ◦ length. That's the composition. Note however two rules:

length ◦ isOdd != isOdd ◦ length
length ◦ toLower = length

OK, at this moment we have some basics of software engineering and you probably already can see some of the characteristics of functional programming languages. But this takes effect not only on functional languages but to imperative and other paradigms too. It's just that functional languages are closer to the math in their notation.

Keep it simple, stupid

Or KISS. My struggle with KISS in pull requests, chats with friends, all over place was the fact that everyone understood that "simple" differently. It meant something slightly different for every one of us. In a sense, what matters is whether one can say anything concrete about that "simple" part? And it appears to be true.

Let's say we have a simple application with five types and four functions:

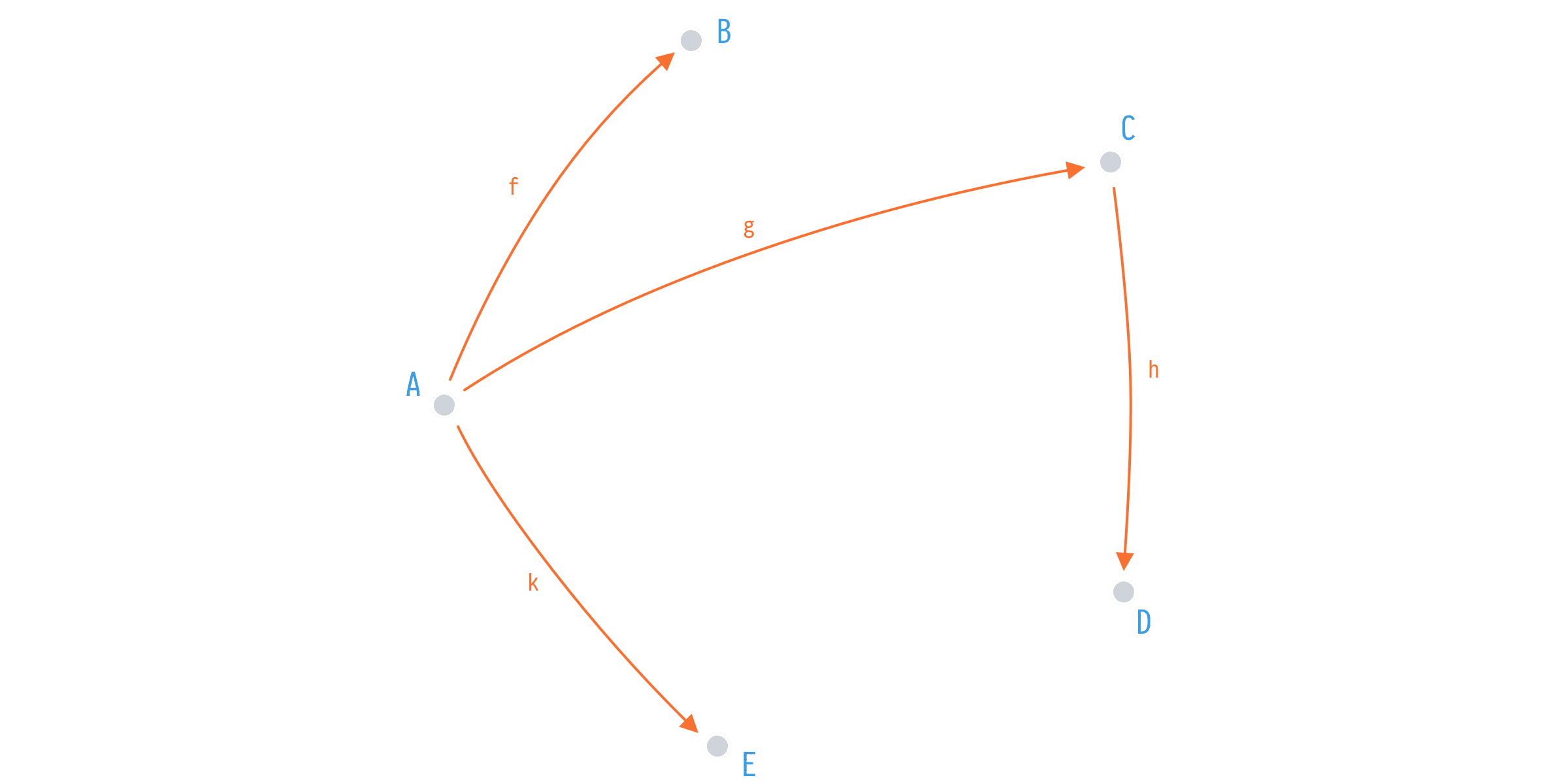
f: A -> B
g: A -> C
k: A -> E
h: C -> D

In this category we have one point of entry (A) and ability to map from that point to others via functions f, g, h, and k. However, we can do even better when it comes to mapping from A to D, we can compose h after g and map those types directly.

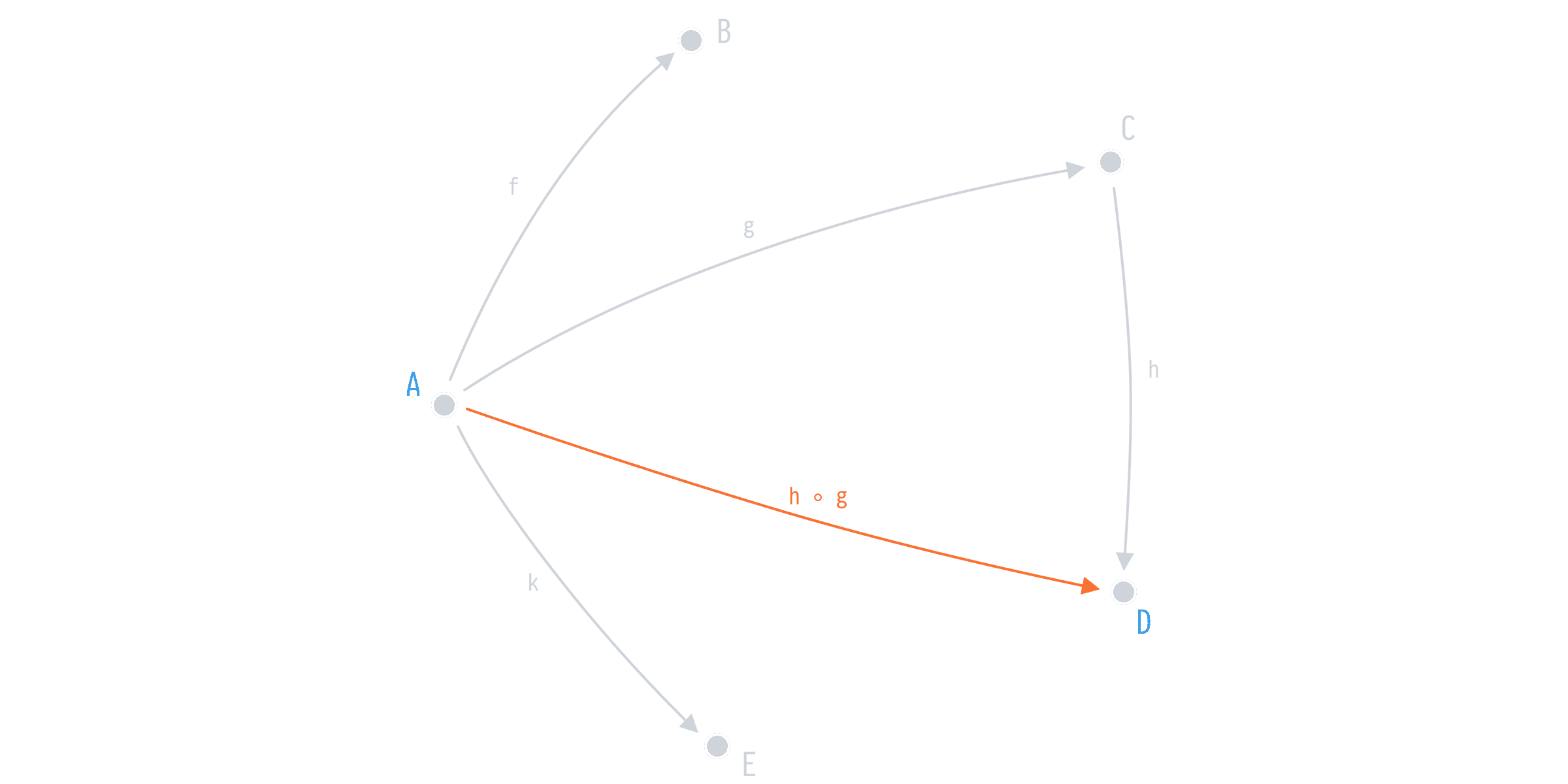
h ◦ g: A -> D

In a sense, we've got h ◦ g for free. And thus are able to easily map from A to D when and if the need comes, say with the next sprint, once your Product Owner decides to show user's (A) invoices (D) based on their payments (C).

But can we write this program in any better way? In a way that it would be easier to modify it, built on top of it? Sure, we can do that too.

Say, we start with the same types and same number of functions but arranged differently

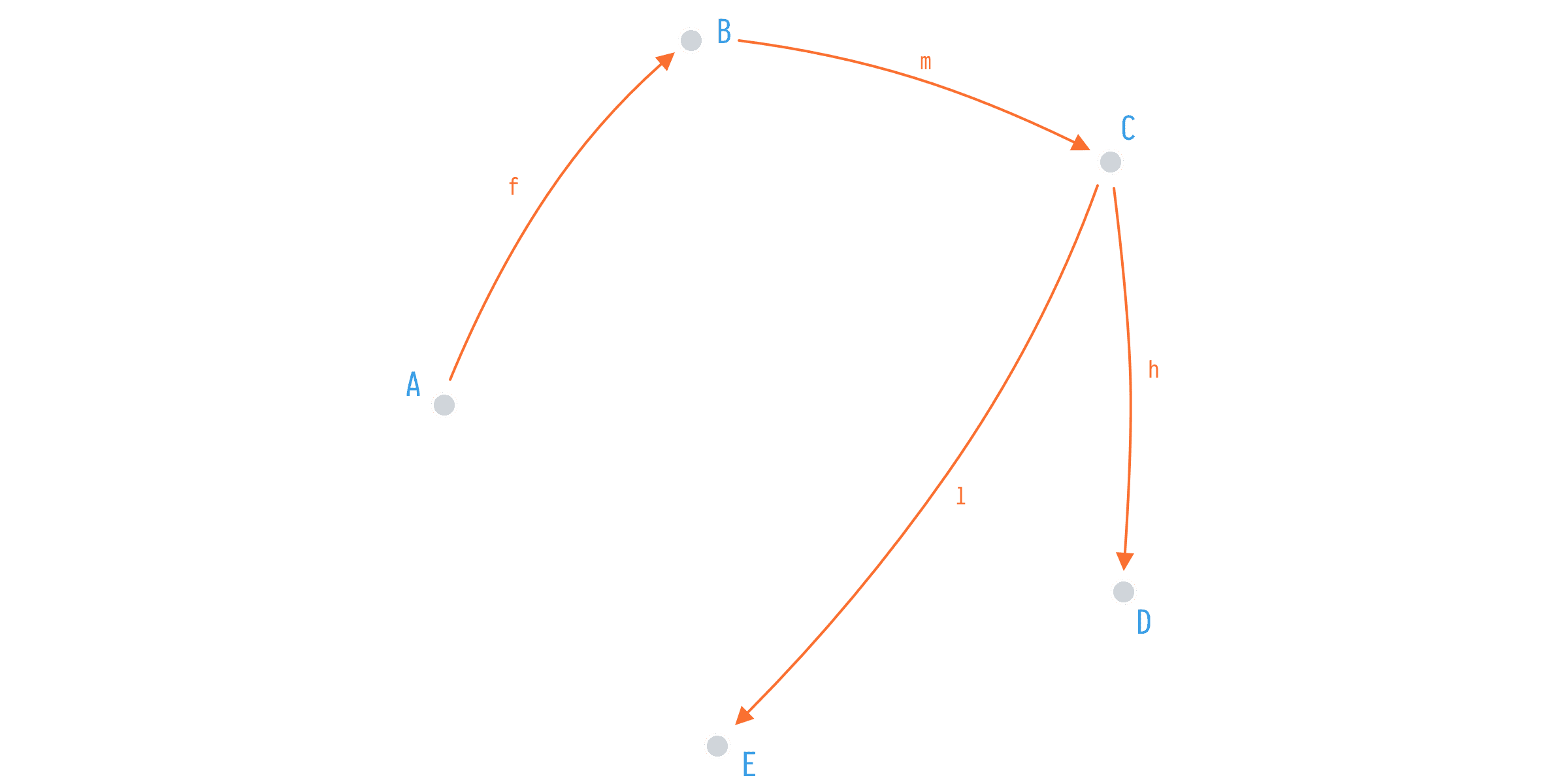
f: A -> B
m: B -> C
l: C -> E
h: C -> D

We've replaced g and k from the first implementation with m and l and at the moment it seems we've lost the ability to map from A to C, and from A to E respectively. But hey, we have a composition.

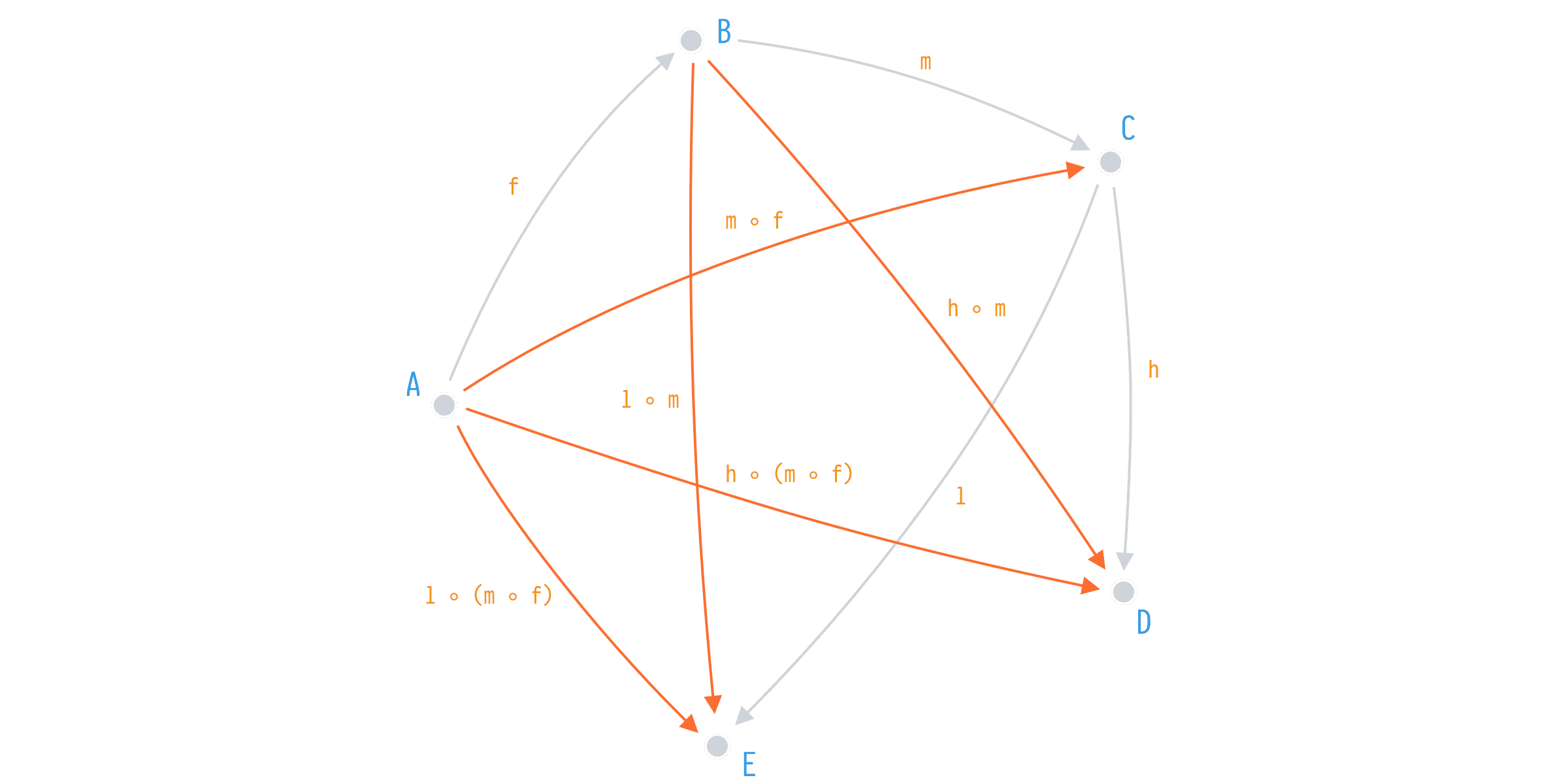
The same number of initial functions on the same objects gives rise to a much more sophisticated system in which we have derived 5(!) new functions. That's 4 more than what we've achieved with the previous example.

m ◦ f: A -> C
h ◦ m: B -> E
l ◦ m: B -> D
l ◦ (m ◦ f): A -> E
h ◦ (m ◦ f): A -> D

What's more, we got those g and k back via composition. g is m ◦ f and k is l ◦ (m ◦ f).

This example illustrates something. Some functions are more composable than others, some applications have functions that are easier to compose to get new functionality. And that's exactly how one can define simplicity

Simpler functions in a given application are those that can be composed in more ways than others.

This is indeed a relative definition, as you need the context of an application. Think of it this way. Given you can write a function a that via composition with other functions in your application produces, say, 10 new possible ways to compose functions. Or, you could write two functions b and c that could be composed with other functions to produce, say, 20 new functions. In general 2 functions b and c would be simpler than one a.

What's next?

Originally, I started thinking about DRY and came to realize that it is in essence talking about beta-equality, which we can explore next time.

I invite you to explore these bits of computer science, there's certainly a sense in which some of the empirical knowledge you have can be formalized and generalized. This certainly can help you in your future endeavors in programming.